Name

PVector
Examples 
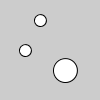
v1 = PVector(40, 20)
v2 = PVector(25, 50)

ellipse(v1.x, v1.y, 12, 12)
ellipse(v2.x, v2.y, 12, 12)
v2.add(v1) # v2 += v1
ellipse(v2.x, v2.y, 24, 24)
Description A class to describe a two or three dimensional vector, specifically a Euclidean (also known as geometric) vector. A vector is an entity that has both magnitude and direction. The datatype, however, stores the components of the vector (x,y for 2D, and x,y,z for 3D). The magnitude and direction can be accessed via the methods mag() and heading().

In many of the Processing examples, you will see PVector used to describe a position, velocity, or acceleration. For example, if you consider a rectangle moving across the screen, at any given instant it has a position (a vector that points from the origin to its location), a velocity (the rate at which the object's position changes per time unit, expressed as a vector), and acceleration (the rate at which the object's velocity changes per time unit, expressed as a vector).

Since vectors represent groupings of values, we'll need to do some "vector" math, which is made easy by the methods inside the PVector class, or, in Python Mode, in some cases the traditional mathematical operators have been "overloaded" to work with PVectors: "+" adds vectors, "-" subtracts vectors, "*" does scalar multiplication, and "/" does scalar division. The related augmented assigment operators, "+=", "-=", "*=", and "/=", also work.
Syntax
	v = PVector(x, y)
	v = PVector(x, y, z)
Parameters
xint: x component of the PVector
yint: y component of the PVector
zint: z component of the PVector
Methods
set() Set the components of the vector
random2D() Make a new 2D unit vector with a random direction.
random3D() Make a new 3D unit vector with a random direction.
fromAngle() Make a new 2D unit vector from an angle
fromAngle() Make a new 2D unit vector from an angle
copy() Get a copy of the vector
mag() Calculate the magnitude of the vector
magSq() Calculate the magnitude of the vector, squared
add() Adds x, y, and z components to a vector, one vector to another, or two independent vectors
sub() Subtract x, y, and z components from a vector, one vector from another, or two independent vectors
mult() Multiply a vector by a scalar
div() Divide a vector by a scalar
dist() Calculate the distance between two points
dot() Calculate the dot product of two vectors
cross() Calculate and return the cross product
normalize() Normalize the vector to a length of 1
limit() Limit the magnitude of the vector
setMag() Set the magnitude of the vector
heading() Calculate the angle of rotation for this vector
rotate() Rotate the vector by an angle (2D only)
lerp() Linear interpolate the vector to another vector
angleBetween() Calculate and return the angle between two vectors
array() Return a representation of the vector as a float array

Updated on Tue Feb 27 14:07:12 2024.

If you see any errors or have comments, please let us know.

Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License